| hard | probability |
An ant is standing on one corner of a cube & can only walk on the edges. The ant is drunk and from any corner, it moves randomly by choosing any edge! What is the expected number of edges the ant travels, to reach the opposite corner?
Try to find the equivalent vertices for the distance yet to travel. This should give equivalent merged vertices, with st being the start & the th being the destination.
We can define equivalent states, based on the corner the Ant is at:
- Starting corner.
- Corner adjacent to the starting corner.
- Corner that shares an edge with the opposite corner.
- The opposite corner.
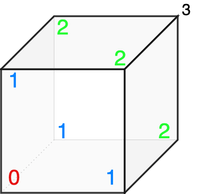
We can represent the expected number of steps from each state as follows:
-
-
-
-
(already reached the destination)
Solving this we find
Calculations:
Substitute and in the middle equation.
