probability puzzles
| medium | probability |
A chess tournament has levels and players with skills . At each level, random pairs are formed and one person from each pair proceeds to the next level. When two opponents play, the one with the better skills always wins. What is the probability that players and will meet in the final level?
if two players meet before the final, they don't meet at the final.
Consider , the probability is 1.
Consider ; the first round can be in the following ways:
They don't meet in finals in the first case (out of a total of three). Thus, for , the probability that they meet is .
Assume that instead of forming random pairs at each level, we have already constructed a "tournament tree", which is a binary tree. At the bottom of this structure, we have the initial players. Each node represents the match between the two children (players), and the value of each node is the player who won that match. The value of the top-level root node is the overall winner of the tournament.
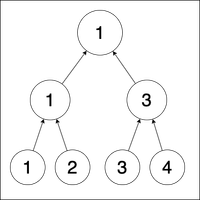
With this image, we can see the whole tournament is deterministic and only depends on the initial arrangement of players (at the bottom level). We also notice that the two players who reach the final level are the best players of the left half of the tree and the right of the tree (respectively).
Imagine players getting partitioned into two groups of players each, with player topping in the first group and player in the second. The best player of each partition reaches the final. The probability that a random partition separates player from is
Here's how: There are empty slots in a sequence at the bottom layer of the tournament tree. We can start assigning players from . Suppose is assigned to a slot in the first half. For , there are total slots remaining, and are in a new group (that does not contain ). Hence, there are favorable choices and total choices.
Hence the probability is
Note: The question says that we are forming random pairs at each level. But that is equivalent to retroactively constructing the bottom-layer of the tournament tree, in any desirable fashion.
For example, consider at the th level, we randomly decide to match with , even though they were not siblings in the tree at that level. That's fine, we can modify the tree such that now and are siblings, while keeping the entire branch below each of those nodes intact.
