medium puzzles
| medium | probability |
p and q are two points chosen at random between 0 & 1. What is the probability that the ratio p/q lies between 1 & 2?
Graph Shading. (Whenever we see two uniform random variables, we graph them up!)
0.25
Assume that the points are & respectively. We want to know if is between 1 and 2. If we plot this, the limits are and . Thus, the desired region is the area between lines & .
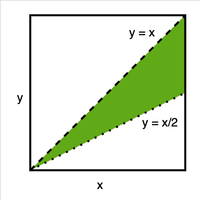
This region is th of the rest.
