deadly puzzles
| deadly | strategy |
Two immensely intelligent players, A & B, engage in a game, the rules of which are as follows. For a natural number , the board consists of numbers from to . Each player takes turns to strike off a (new) number from the board. But, to make sure doesn't affect who wins, there is an added rule. Once you strike off a number, you also have to strike off all its divisors in that same chance, irrespective of whether any of those divisors were already marked. The player to strike off the last number on the board wins.
Can A construct a winning strategy?
Note: The question asks for the existence of the strategy, not to devise the strategy itself.
Can one player copy the strategy of the other?
For a given , either has a winning strategy or . If has the strategy, then can strike 1 and copy 's strategy.
There is no simple winning strategy, based on the initial number , that A can use to win the game. We'll use the common strategy stealing argument.
Determinism
The game can be represented as a tree, where each node represents a possible state of the game, and the children represent valid moves to the next states.
For instance, for , the root node is (5, 4, 3, 2, 1). There will be children nodes directly from the root node, and so on.
Let "level" be the number of turns completed so far.
At level , we have the root node. All the states that can be reached by striking one number (and its divisors) are at level 1. And so on.
The height of the tree is at most (finite).
Many nodes might hold the same state. All the leaf nodes look like empty sets where all numbers are struck off. (5, 4, 3, 2, 1). If this node is at an odd level then player has won. Otherwise, the player has won.
Let's color our game tree to represent the winning player in each possible end state. We color a leaf node "red" if the end state it represents is a win for Player , and blue if it's a win for Player . All leaf nodes at odd levels are red. And those at even levels are blue.
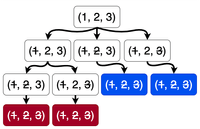
Note that both players will try to move rationally toward their favored colored children nodes. Hence we can propagate these colors up. We consider the following cases:
-
If all children of a node are red, then that node itself becomes red, regardless of the level (odd or even). Same for blue.
-
If a node has both red and blue children, it depends on the player. If it is at an even level, then it is Player 's turn. Otherwise, Player is in control. If a node at an even level has at least one red child node, then we can color this node as red, and delete the blue children nodes. This is because Player will rationally move towards the winning state only. Similarly, we can propagate the blue nodes.
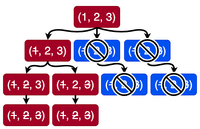
Thus, we can completely color the entire tree including the root node. It will either be entirely red or entirely blue. This means that if both the players are rational geniuses, the winner is predetermined from the value of .
Existence of a Winning Strategy
Now, we examine the color of the root node. If it's red, Player has a winning strategy right from the start. But can it be blue?
Let's investigate this in detail. From the root node, there can be children, associated with striking each corresponding number. Consider all children associated with strike the number , where . If any one of these children is red, then the root node must be red. But if all are blue, that means that Player can force a win from any of these states. In other words, regardless of what player strikes ( to ), player can push the game into a guaranteed win for player .
But wait! There's a special move Player can make: striking out 1. Thus, Player is put into the same position Player was in at the start. From here, player B can choose to strike a number from to , and player can force a win from here on, by copying the strategy of player .
The special state (1, 2,..., N) is only accessible from the root node. Because of an extra node, all the level numbers switch from odd to even and vice versa. Incidentally, this subtree will look exactly like the root tree with reverse colors (and also with one subtree cut-off, corresponding to this node). Thus, the root of the subtree representing this new game state is red because all the nodes from this point forward are red.
In conclusion, Player always has a winning strategy in the Game of Divisors. By either making a move that leads directly to a winning game state or by striking out 1 and then mirroring Player 's ideal moves to force a win.
This is a non-constructive strategy.
Script
Using a script to generate the first move for a few values of .
Find the Colab Script here.
| First move | |
|---|---|
| 1 | 1 |
| 2 | 2 |
| 3 | 1 |
| 4 | 2 |
| 5 | 4 |
| 6 | 6 |
| 7 | 1 |
| 8 | 7 |
| 9 | 7 |
| 10 | 6 |
Indeed, the first player always wins, but has to often start by striking .
